Wie funktioniert der Levenshtein-Algorithmus...?
Der Levenshtein-Algorithmus (auch Edit-Distanz genannt) errechnet
die Mindestanzahl von Editierungsoperationen, die notwendig sind,
um eine bestimmte Zeichenkette soweit abzuändern, um eine andere
bestimmte Zeichenkette zu erhalten. Die wohl bekannteste Weise
die Edit-Distanz zu berechnen erfolgt durch den sogenannten Dynamic-Programming-Ansatz.
Dabei wird eine Matrix initialisiert, die für jede (m, N)-Zelle
die Levenshtein-Distanz (levenshtein distance) zwischen dem m-Buchstabenpräfix
des einen Wortes und des n-Präfix des anderen Wortes enthält.
Die Tabelle kann z.B. von der oberen linken Ecke zur untereren
rechten Ecke gefllt werden. Jeder Sprung horizontal oder vertikal
entspricht einer Editieroperation (Einfügen bzw. Löschen eines
Zeichens) und "kostet" einen bestimmte virtuellen Betrag. Die
Kosten werden normalerweise auf 1 für jede der Editieroperationen
eingestellt. Der diagonale Sprung kostet 1, wenn die zwei Buchstaben
in die Reihe und Spalte nicht bereinstimmen, oder im Falle einer
Übereinstimmung 0. Jede Zelle minimiert jeweils die lokalen Kosten.
Daher entspricht die Zahl in der untereren rechten Ecke dem Levenshtein-Abstand
zwischen den beiden Wörtern. Hier ist ein Beispiel, das den Vergleich
von "meilenstein" und "levenshtein" kennzeichnet:
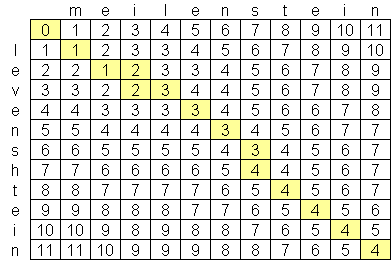
Es gibt zwei mögliche Wege durch das Tableau, die die geringsten Kosten produzieren. Nämlich

"=" Übereinstimmung; "o" Ersetzen; "+" Einfügen; "-" Löschen
Obwohl ausgeklügelte Verbesserungen bezglich der Berechnung
grosser Matrizen gemacht wurden, gibt es keine Alternative zu
dem meist recht großen Berechnungsaufwand. Nachdem Kenntnisstand der
Autoren gelanges bisher nur der Firma Exorbyte
den Levensthein Algorithmus in höchster
Geschwindigkeit zu implementieren.
|
|
|